居然是全省第二 (广东 B 组省一共 91 人，前 2.1%)，差点没把我笑死

运气成分比较多，当时比赛的时候只做对了 A、C、I，然后在 D、F、J 混了点分 (本题解是赛后思考修正的)，归功于 I 的分值比较高又刚好会做哈哈

测试链接：https://www.dotcpp.com/oj/train/1093/

A：2023 100🏆

【问题描述】

请求出在 12345678 至 98765432 中，有多少个数中完全不包含 2023 。

完全不包含 2023 是指无论将这个数的哪些数位移除都不能得到 2023 。

例如 20322175，33220022 都完全不包含 2023，而 20230415，20193213 则含有 2023 (后者取第 1, 2, 6, 8 个数位) 。

【解析及代码】

数据规模也才 1e9 左右，暴力枚举就完了

利用 re 库的正则表达式进行匹配，非常方便，答案：85959030

import re

pat = re.compile(r'\d*'.join('2023'))
nums = range(12345678, 98765432 + 1)
print(sum(not re.search(pat, i) for i in map(str, nums)))

B：硬币兑换 100🏆

【问题描述】

小蓝手中有 2023 种不同面值的硬币，这些硬币全部是新版硬币，其中第 i (1 ≤ i ≤ 2023) 种硬币的面值为 i ，数量也为 i 个。硬币兑换机可以进行硬币兑换，兑换规则为：交给硬币兑换机两个新版硬币 coin1 和 coin2 ，硬币兑换机会兑换成一个面值为 coin1 + coin2 的旧版硬币。

小蓝可以用自己已有的硬币进行任意次数兑换，假设最终小蓝手中有 K 种不同面值的硬币（只看面值，不看新旧）并且第 i (1 ≤ i ≤ K) 种硬币的个数为 $sum_i$ 。小蓝想要使得 $\max\{sum_1, sum_2, \cdots, sum_K\}$ 的值达到最大，请你帮他计算这个值最大是多少。

注意硬币兑换机只接受新版硬币进行兑换，并且兑换出的硬币全部是旧版硬币。

【解析及代码】

第一种思路是，根据面值 2023 的硬币数最多，直接尽可能地兑换面值 2023 的旧硬币，总数为： $2023 + \frac{(1+1011)\times1011}{2}=513589$

上述方法在兑换时使用的最大面值为 $r = 1011$ (因为用 1011 和 1012 凑成 2023 时，数量取决于 1011，所以不考虑 1012)，最优的凑法是凑成面值 2023 (= 1011 × 2 + 1) 的旧硬币

第二种思路是，枚举用于兑换的新硬币最大面值 $r \in [1012, 2023)$ ，并兑换面值为 $tar = 2r + 1$

对于每一组 $l,r$ ，可以兑换面值为 $tar$ 的旧硬币的个数为 $\frac{(l+r)(r-l+1)}{2}$ ，不难推导出这是个关于 r 的二次函数，也就是其有极大值

枚举 r 并进行求解，最大值为：682425

ans = 0
for r in range(1012, 2023):
    # 目标面值
    tar = r * 2 + 1
    l = tar - 2023
    tmp = (l + r) * (r - l + 1) // 2
    # 无更优时退出
    if tmp < ans: break
    ans = tmp
    print(l, r, tmp)
print(ans)

C：松散子序列 91🏆

【问题描述】

给定一个仅含小写字母的字符串 s ，假设 s 的一个子序列 t 的第 i 个字符对应了原字符串中的第 $p_i$ 个字符。我们定义 s 的一个松散子序列为：对于 i > 1 总是有 $p_i - p_{i-1} \geq 2$ 。设一个子序列的价值为其包含的每个字符的价值之和 (a ∼ z 分别为 1 ∼ 26) 。

求 s 的松散子序列中的最大价值。

【输入格式】

输入一行包含一个字符串 s 。

【输出格式】

输出一行包含一个整数表示答案。

【样例】

输入	输出
azaazaz	78

【评测用例规模与约定】

20%	$\|s\| \leq 10$
40%	$\|s\| \leq 300$
70%	$\|s\| \leq 5000$
100%	$1 \leq \|s\| \leq 10^6$ ，字符串中仅包含小写字母

【解析及代码】

先利用 ord 函数，将小写字母转化为 1 ~ 26 的值，记为 value

创建一维列表 dp，以 dp[i] 表示第 i 个字符 (索引从 1 开始) 被包含时，松散子序列的最大价值

然后以 value = [1, 26, 1, 1, 1, 26, 1, 26] 为例：

当第 6 个字符 (第 2 个 26) 被包含时，因为松散子序列的定义有 dp[6] = max(dp[:5]) + 26
然后又因为题目要求的是价值最大的松散子序列，所以被包含的字符之间的空隔不超过 2，此时可以进一步减少计算量，有 dp[6] = max(dp[3: 5]) + 26

value = list(map(lambda s: ord(s) - 96, input()))
# dp[i] 表示第 i 个字符被采用时的最高分数
dp = [0] * (len(value) + 1)
dp[1] = value[0]

for i, v in zip(range(2, len(value) + 1), value[1:]):
    # 找到最优的前置状态: 最优松散子序列中各个数的间隔不超过 2
    dp[i] = max(dp[max((0, i - 3)): i - 1]) + v
# 最后两个数必有一个被包含
print(max(dp[-2:]))

D：管道 73🏆

【问题描述】

有一根长度为 len 的横向的管道，该管道按照单位长度分为 len 段，每一段的中央有一个可开关的阀门和一个检测水流的传感器。

一开始管道是空的，位于 $L_i$ 的阀门会在 $S_i$ 时刻打开，并不断让水流入管道。

对于位于 $L_i$ 的阀门，它流入的水在 $T_i (T_i \geq S_i)$ 时刻会使得从第 $L_i - (T_i - S_i)$ 段到第 $L_i + (T_i - S_i)$ 段的传感器检测到水流。

求管道中每一段中间的传感器都检测到有水流的最早时间。

【输入格式】

输入的第一行包含两个整数 n, len，用一个空格分隔，分别表示会打开的阀门数和管道长度。

接下来 n 行每行包含两个整数 $L_i, S_i$ ，用一个空格分隔，表示位于第 $L_i$ 段管道中央的阀门会在 $S_i$ 时刻打开。

【输出格式】

输出一行包含一个整数表示答案。

【样例】

输入

输出

3 10

1 1

6 5

10 2

【评测用例规模与约定】

30%	$n \leq 200, S_i, len \leq 3000$
70%	$n \leq 5000, S_i, len \leq 10^5$
100%	$1 \leq n \leq 10^5, 1 \leq S_i, len \leq 10^9, 1 \leq L_i \leq len, L_{i-1} < L_i$

【解析及代码】

看不懂为什么会运行错误 ……

把水的流动过程划分为两个过程，即从左到右流动 + 从右到左流动，为每个过程的每段管道计算最早检测到水流的时间 (耗时约 $2\ len$ )

再考虑水是双向流动的，某一段管道有水的最早时间就是对这两个过程求最小值 (耗时约 $len$ )，最大值即为答案 (耗时约 $len$ )

这样的思路总耗时约为 $4\ len$ ，而暴力遍历的耗时约为 $n\ len$ (测评分数为 36)

n, length = map(int, input().split())
info = [list(map(int, input().split())) for _ in range(n)]
# 使所有阀门的位置 -1
for i in range(n): info[i][0] -= 1
# 按阀门的位置进行排序
info.sort(key=lambda x: x[0])


def solve():
    t = [float('inf')] * length
    for i in range(n - 1):
        (l1, s1), (l2, s2) = info[i: i + 2]
        # 修正该阀门的开始时间, 即左侧有水的时间 + 1
        s1 = min((t[l1 - 1] + 1, s1))
        # 使进入阀门的水只向着右侧流动
        for j in range(l2 - l1): t[l1 + j] = s1 + j
    # 打开最后一个阀门
    lf, sf = info[-1]
    sf = min((t[lf - 1], sf))
    for j in range(length - lf): t[lf + j] = sf + j
    return t


# 水流从左侧流向右侧
l2r = solve()
# 水流从右侧流向左侧
info.reverse()
for i in range(n): info[i][0] = length - 1 - info[i][0]
r2l = reversed(solve())
# 组合得到管道每个位置开始有水流的时间
print(max(map(min, zip(l2r, r2l))))

E：保险箱 18🏆

【问题描述】

小蓝有一个保险箱，保险箱上共有 n 位数字。

小蓝可以任意调整保险箱上的每个数字，每一次操作可以将其中一位增加 1 或减少 1。

当某位原本为 9 或 0 时可能会向前（左边）进位/退位，当最高位（左边第一位）上的数字变化时向前的进位或退位忽略。

例如：

00000 的第 5 位减 1 变为 99999 ；

99999 的第 5 位减 1 变为 99998 ；

00000 的第 4 位减 1 变为 99990 ；

97993 的第 4 位加 1 变为 98003 ；

99909 的第 3 位加 1 变为 00009 。

保险箱上一开始有一个数字 x，小蓝希望把它变成 y，这样才能打开它，问小蓝最少需要操作的次数。

【输入格式】

输入的第一行包含一个整数 n 。

第二行包含一个 n 位整数 x 。

第三行包含一个 n 位整数 y 。

【输出格式】

输出一行包含一个整数表示答案。

【样例】

输入

输出

12349

54321

【评测用例规模与约定】

30%	$1 \leq n \leq 300$
60%	$1 \leq n \leq 3000$
100%	$1 \leq n \leq 10^5$ ，x,y 中仅包含数字 0 至 9，可能有前导零

【解析及代码】

想了一整天都没想出来问题出在哪，点到为止 (大佬们帮我看看我的思路有什么漏洞)

从题目的样例可以看到，低位的操作会影响高位的数字，但是高位的操作不会影响低位的数字，所以我们可以从低位开始调整保险箱的数字

低位的操作可能会导致高位：

进位 (e.g., 597 → 591)：597 → 601 → 591 需要 4 步，597 → 591 需要 6 步
退位 (e.g., 591 → 597)：591 → 587 → 597 需要 5 步，591 → 597 需要 6 步

不难归纳出，低位的调整无需考虑对高位的影响，只需贪心地选择步数最少的方向即可

但是当向上调整的步数、向下调整的步数相等时，则需要考虑对高位的影响 (e.g., 596 → 601)

n = int(input())
# 新增数位, 保留前导零
x = int('1' + input())
y = int(input())

t = 0
# 从低位开始操作
for i in range(n):
    # 取最后一位数字记为 a
    ax, ay = x % 10, y % 10
    # a 上下调整所需的次数
    up = (ay - ax) % 10
    down = 10 - up
    t += min((up, down))
    # 两者不相等
    if up != down:
        x += up if up < down else -down
    # 两者相等 (up=down=5), 考虑高位
    else:
        # 取末 2 位数字记为 b
        bx, by = x % 100, y % 100
        # 计算上下调整后的误差
        fe = lambda e_: min((e_, 10 - e_))
        eup = fe((bx + 5 - by) % 100 // 10)
        edown = fe((bx - 5 - by) % 100 // 10)
        # 根据误差进行调整
        x += 5 if eup < edown else -5
    # 令保险箱忽略最后一位
    x, y = x // 10, y // 10
print(t)

F：树上选点 100🏆

【问题描述】

给定一棵树，树根为 1，每个点的点权为 $V_i$ 。

你需要找出若干个点 $P_i$ ，使得：

1. 每两个点 $P_x, P_y$ 互不相邻；

2. 每两个点 $P_x, P_y$ 与树根的距离互不相同；

3. 找出的点的点权之和尽可能大。

请输出找到的这些点的点权和的最大值。

【输入格式】

输入的第一行包含一个整数 n 。

第二行包含 n − 1 个整数 $F_i$ ，相邻整数之间使用一个空格分隔，分别表示第 2 至 n 个结点的父结点编号。

第三行包含 n 个整数 $V_i$ ，相邻整数之间使用一个空格分隔，分别表示每个结点的点权。

【输出格式】

输出一行包含一个整数表示答案。

【样例】

输入

输出

1 2 3 2

2 1 9 3 5

【评测用例规模与约定】

40%	$n \leq 5000$
100%	$1 \leq n \leq 2 \times 10^5, 1 \leq F_i < i, 1 \leq V_i \leq 10^4$

【解析及代码】

编写继承 list 的类 Node，用于存储子结点的序号，并用实例变量 i, f, v 分别记录序号、父结点、点权

从根结点出发，搜索并得到各个结点的深度 (即与树根的距离)，并根据深度添加到字典 depths

因为要选取若干个点，所以在树足够大的时候树的每一层都会有一个点被选取

而又要求点与点之间互不相邻，所以又会有一些层没有点被选取

以 $dp[i][j]$ 表示从根结点出发，选中第 i 层第 j 个结点时可以得到的最大点权和，那么有：

$dp[i][j]=\max (\max dp[i-2], \max dp[i-1]) + V_{ij}$

其中的 $\max dp[i-1]$ 又需要加上“是否相邻”的判断，不难看出这是一个动态规划问题

为了进一步优化 $\max$ 运算，又可以将 $dp[i]$ 进行降序排序，以确保 $dp[i][0]$ 就是最大值

class Node(list):
    ''' 元素: 子结点序号
        i: 自身序号
        f: 父结点序号
        v: 结点权值
        ret: 从根结点出发选点, 选中该点时可以得到的最大点权和'''

    def __init__(self, i, f, v):
        super().__init__()
        self.i = i
        self.f = f
        self.v = v
        self.ret = 0


_ = int(input())
nodes = [Node(i, f, v) for i, (f, v) in enumerate(zip([-1] + list(map(lambda x: int(x) - 1, input().split())),
                                              map(int, input().split())))]
# 添加子结点
for n in nodes[1:]: nodes[n.f].append(n.i)

# 各个深度的结点的字典
depths = {-1: [Node(-1, -1, 0)]}
# 使用栈消除递归: 结点, 深度
stack = [(nodes[0], 0)]
while stack:
    n, d = stack.pop()
    depths.setdefault(d, []).append(n)
    # 子结点入栈
    stack += [(nodes[j], d + 1) for j in n]

maxd = len(depths) - 2
# 设置空结点、根结点的搜索值, 开始动态规划
depths[0][0].ret = depths[0][0].v
# 按深度递增的顺序搜索
for d in range(1, maxd + 1):
    for ni in depths[d]:
        # 取 d-2 层的最优状态
        ni.ret = depths[d - 2][0].ret + ni.v
        # 搜索 d-1 层的最优状态 (ni 不能是 nj 的子结点)
        for nj in filter(lambda nj: ni.f != nj.i, depths[d - 1]):
            ni.ret = max((ni.ret, nj.ret + ni.v))
            break
    # 根据搜索值进行排序
    depths[d].sort(key=lambda n: n.ret, reverse=True)

print(max((depths[maxd][0].ret, depths[maxd - 1][0].ret)))

G：T 字消除

【问题描述】

小蓝正在玩一款游戏，游戏中有一个 n × n 大小的 01 矩阵 $A_{i, j}$ 。

小蓝每次需要选择一个 T 字型的区域，且这个区域内至少要有一个 1 。选中后，这个区域内所有的元素都会变成 0 。

给定游戏目前的矩阵，小蓝想知道他最多可以进行多少次上述操作。

T 字型区域是指形如 (x − 1, y) (x, y) (x + 1, y) (x, y + 1) 的四个点所形成的区域。其旋转 90, 180, 270 度的形式同样也视作 T 字形区域。

【输入格式】

输入包含多组数据。

输入的第一行包含一个整数 D 表示数据组数。

对于每组数据，第一行包含一个整数 n 。

接下来 n 行每行包含 n 个 0 或 1，表示矩阵 $A_{i,j}$ 的每个位置的值。

【输出格式】

输出 D 行，每行包含一个整数表示小蓝最多可以对当前询问中的矩阵操作的次数。

【样例】

输入

输出

说明

1 3

001

011

111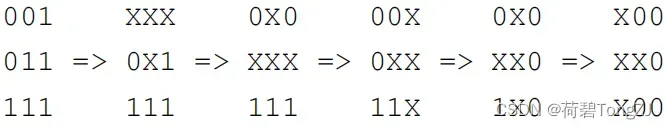

【评测用例规模与约定】

10%	$n=3$
40%	$n \leq 30$
100%	$3 \leq n \leq 2000$

【解析及代码】

H：独一无二

【问题描述】

有一个包含 n 个点，m 条边的无向图，第 i 条边的边权为 $c_i$ ，没有重边和自环。设 $s_i$ 表示从结点 1 出发到达结点 i 的最短路的不同路径数 (i ∈ [1, n])，显然可以通过删除若干条边使得 $s_i = 1$ ，也就是有且仅有一条从 1 到 i 的最短路，且保持最短路的路径长度不变，对于每个 i ，求出删除边数的最小值。

【输入格式】

输入的第一行包含两个正整数 n, m。接下来 m 行，每行包含三个正整数 $u_i, v_i, c_i$ 表示第 i 条边连接的两个点的编号和边权。

【输出格式】

输出 n 行，第 i 行包含一个正整数表示对于结点 i ，删除边数的最小值，如果 1 和 i 不连通，输出 −1 。

【样例】

输入

输出

说明

4 4

1 2 1

1 3 2

2 4 2

3 4 1

在给定的图中，只有 $s_4$ 一开始为 2，

因为有两条最短路：1 → 2 → 4, 1 → 3 → 4，

任意删掉一条边后，就可以只剩一条最短路。

【评测用例规模与约定】

30%	$n \leq 1000$
100%	$n \leq 10^5, 0 \leq m \leq \min\{\frac{n(n-1)}{2}, 10^6\}, 1 \leq u_i, v_i \leq n, 1 \leq c_i \leq 10$

【解析及代码】

I：异或和 28🏆

【问题描述】

给一棵含有 n 个结点的有根树，根结点为 1 ，编号为 i 的点有点权 $a_i (i \in [1, n])$ 。现在有两种操作，格式如下：

1 x y 该操作表示将点 x 的点权改为 y 。
2 x 该操作表示查询以结点 x 为根的子树内的所有点的点权的异或和。

现有长度为 m 的操作序列，请对于每个第二类操作给出正确的结果。

【输入格式】

输入的第一行包含两个正整数 n, m ，用一个空格分隔。

第二行包含 n 个整数 $a_1, a_2, \cdots, a_n$ ，相邻整数之间使用一个空格分隔。

接下来 n − 1 行，每行包含两个正整数 $u_i, v_i$ ，表示结点 $u_i$ 和 $v_i$ 之间有一条边。

接下来 m 行，每行包含一个操作。

【输出格式】

输出若干行，每行对应一个查询操作的答案。

【样例】

输入

输出

4 4

1 2 3 4

1 2

1 3

2 4

2 1

1 1 0

2 1

2 2

【评测用例规模与约定】

30%	$n,m \leq 1000$
100%	$1 \leq n, m \leq 10^5, 0 \leq a_i, y \leq 10^5, 1 \leq u_i, v_i,x \leq n$

【解析及代码】

先看看异或这个操作的特性，比如 7(111) ^ 4(100) = 3(011)，3(011) ^ 7(111) = 4(100)

所以，对于一个数组的异或和，如果其中的某一个数值被改变，异或上原来的数值、新的数值即可得到新的异或和

利用这个技巧，可以在初始化的时候预计算所有子树的异或和，并在每次更新点权时更新所有父结点的异或和

定义 Node 类，以存储树结点的信息，并进行异或和的计算：

search：因为题目给定的是“边”，所以只能知道每个树结点与哪个结点相连，而不知道父结点；从根结点开始搜索，利用这个函数可以找到所有树结点的父结点，并预计算异或和
update：递归函数，给当前结点、所有父结点的异或和异或上参数 v
change：调用 update 函数修改异或和，并修改当前结点的 v

class Node:

    def __init__(self, info):
        super().__init__()
        # 父结点, 子结点
        self.dad = None
        self.vex = set()
        # 索引, 价值, 子树异或和
        self.i, self.v = info
        self.sum = self.v

    def search(self, dad):
        # 设置父结点
        self.dad = dad
        self.vex.remove(dad)
        # 计算子树异或和
        for child in self.vex:
            self.sum ^= nodes[child].search(self.i)
        delattr(self, 'vex')
        return self.sum

    def change(self, v):
        self.update(v ^ self.v)
        self.v = v

    def update(self, v):
        self.sum ^= v
        if self.dad >= 0:
            nodes[self.dad].update(v)


n, m = map(int, input().split())
nodes = list(map(Node, enumerate(map(int, input().split()))))
# 添加父结点、子结点
for _ in range(n - 1):
    u, v = map(lambda x: int(x) - 1, input().split())
    nodes[u].vex.add(v)
    nodes[v].vex.add(u)
# 查找父结点, 计算异或和
nodes[0].vex.add(-1)
nodes[0].search(-1)
# 开始若干次操作
for _ in range(m):
    oper, *args = map(int, input().split())
    if oper == 1:
        x, y = args
        nodes[x - 1].change(y)
    else:
        print(nodes[args[0] - 1].sum)

J：混乱的数组 100🏆

【问题描述】

给定一个正整数 x，请找出一个尽可能短的仅含正整数的数组 A 使得 A 中恰好有 x 对 i, j 满足 $A_i > A_j$ 。如果存在多个这样的数组，请输出字典序最小的那个。

【输入格式】

输入一行包含一个整数表示 x 。

【输出格式】

输出两行。

第一行包含一个整数 n ，表示所求出的数组长度。

第二行包含 n 个整数 $A_i$ ，相邻整数之间使用一个空格分隔，依次表示数组中的每个数。

【样例】

输入

输出

3 2 1

【评测用例规模与约定】

30%	$x \leq 10$
60%	$x \leq 100$
100%	$1 \leq x \leq 10^9$

【解析及代码】

题目不是很完整的样子，需要我们自行推导一下附加条件

根据样例可知，[3 2 1] 包含 3 对 $A_i > A_j$ ，而且 $i < j$

显然可得，长度为 n、元素从 n 到 1 的正整数数组可以提供的“对”数为： $\frac{(n-1)n}{2} \geq x$

那么可解得 $n = \left \lceil \sqrt{2x+\frac{1}{4}}+\frac{1}{2} \right \rceil$ ，对于 x = 11，该数组就为 [6 5 4 3 2 1]

上述数组实际提供的“对”数为 15，溢出的 4 对可以通过减小数组的值抹去

除去“对”数	混乱数组
0	6 5 4 3 2 1
1	5 4 3 2 1 1
2	4 3 2 2 1 1
3	3 3 2 2 1 1
4	2 4 3 2 1 1

因为要求字典序最小，所以每一次除去“对”都要尽量使得第一位 -1 (为什么不是 -2 可以自己推一下)

记 $A_i$ 的贡献度为 $A_i > A_j (i < j)$ 的对数，则 6 5 4 3 2 1 中的 4 的贡献度为 3

以 6 5 4 3 2 1 → 5 4 3 2 1 1 为例，使其中的 2 的贡献度 -1，并保持其它数字的贡献度不变，则可以使得总贡献度 (总“对”数) -1

但有一种特殊情况，即 3 3 2 2 1 1 → 2 4 3 2 1 1，3 的变化会使其贡献度 -2，需要使 2 的贡献度 +1

所以出现了除去“对”数为 1、4 时，数组元素除首位之外是相同的

再推导 x = 16 的情况，以进一步总结规律：

除去“对”数	混乱数组
0	7 6 5 4 3 2 1
1	6 5 4 3 2 1 1
2	5 4 3 2 2 1 1
3	4 3 3 2 2 1 1
4	3 4 3 2 2 1 1
5	2 5 4 3 2 1 1

根据所需除去的“对”数，可以推导出数组的首位；根据数组的长度 n、元素的位置，又可以求出数组的其它值 (找规律很简单的啦，不懂就看看代码)

import math

x = int(input())
# (n - 0.5) ^ 2 = 2x + 0.25
n = math.ceil(math.sqrt(2 * x + 0.25) + 0.5)
array = list(range(n, 0, -1))
# 溢出的 "对" 数
overflow = (n - 1) * n // 2 - x

array[0] -= overflow
# 不考虑数组首位, 等价的溢出 "对" 数
overflow = round((n - 1) / 2 - abs((n - 1) / 2 - overflow))
for i in range(1, n):
    lowlim = (i + 1) // 2
    array[-i] = max((array[-i] - overflow, lowlim))

print(n)
print(*array)

文章出处登录后可见！

已经登录？立即刷新

蓝桥杯【第14届省赛】Python B组 76.10分

A：2023 100🏆

B：硬币兑换 100🏆

C：松散子序列 91🏆

D：管道 73🏆

E：保险箱 18🏆

F：树上选点 100🏆

G：T 字消除

H：独一无二

I：异或和 28🏆

J：混乱的数组 100🏆

相关推荐