1 通俗解释

  定义：对于任意可逆方阵，存在一个向量，用该矩阵乘以该向量后，向量的大小发生变化而方向不变。也就是说，对于矩阵，存在一个非的维向量使下式成立：

其中，比例系数成为矩阵的特征值，向量成为该特征值对应的特征向量。
对于一个可逆方阵可以存在一组特征值与特征向量。将上面的公式简化之后为：

其中是矩阵值特征向量是特征值。特征值是一个数字，而向量的数乘本质上是向量的缩放。如， ， 则。变换后与原向量相比向量的大小变为原来的两倍而方向没有发生变化。再由于上面的二式左右相等，因此矩阵乘以一个向量的效果是让该向量进行了一个方向不变的伸缩。【参考文献1】
所以特征值和特征向量的通俗解释是:

1. 矩阵是一个向量的变换方式。
2. 特征向量就是该向量经过某一矩阵变换之后其方向不变的向量。
3. 特征值是一个伸缩倍数。

这里再补充一下特征值和特征向量的性质：
特征值：是阶矩阵是的个特征值则有：

特征向量:阶矩阵的互不相等的特征值对应的特征向量线性无关。

2 矩阵从运动的角度理解

  如果阅读过理解矩阵（一）（二）（三）系列的文章，可以从变换的角度理解特征值与特征向量。以为例介绍矩阵的含义 ：

• 从变换的角度来说，矩阵可以理解为对向量做变换得到了
• 从坐标系的角度来说，可以理解成是一个坐标系（常用的坐标是笛卡尔坐标系，即），向量就是在这个坐标系下的坐标，对应到坐标系下的坐标是向量。

  那特征值和特征向量具体是什么含义呢？
  我们假设矩阵的某个特征值为, 对应的特征向量是。根据定义和上面对矩阵的理解可以知道，是以为坐标系的坐标向量，将其变换到以为坐标系后得到的坐标向量 与 它原来的坐标向量 永远存在一个 倍的伸缩关系。
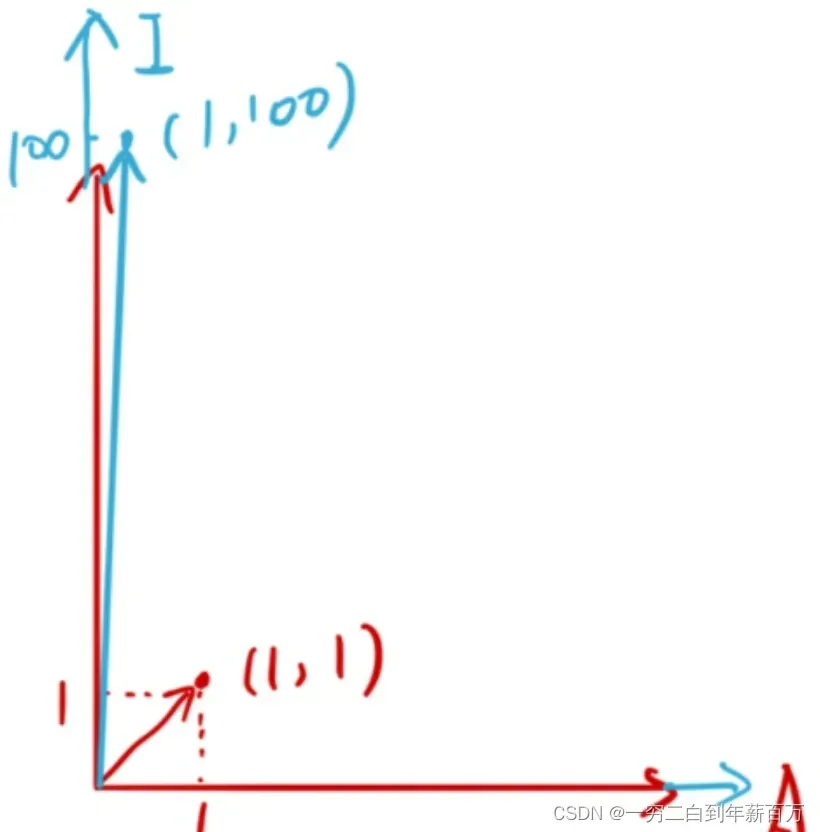
  为了方便理解举一个简单的例子，假如矩阵如下，可以看到它的特征值有个，分别是，分别对应个特殊的特征向量，即。

  所以矩阵左乘任意的一个向量，其实都可以理解成是把向量沿着这个特征向量的方向进行伸缩，伸缩比例就是对应的特征值。可以看到这个特征值差别是很大的，最小的只有，最大的特征值为。

3 特征值和特征向量的意义

  意义就在于如果我们知道了特征值的大小，有时为了减少计算了，我们可以只保留特征值较大的，比如上面的图片中，我们可以看到变换后的向量轴适合原来一样的，而轴方向拉伸了倍，所以通常为了实现压缩算法，我们可以只保留轴方向的变换即可。 对应到高维情况也是类似的，多维矩阵会把向量沿着多个方向拉伸，有的方向可能拉伸幅度很小，而有的很大，我们只需要保留幅度大的即可达到压缩的目的。【参考文献3】

4 从计算的角度理解

  举个例子：矩阵的特征值为，特征向量为。

假设存在向量。下面采用另一种方法计算：首先将表示成特征向量的线性组合

然后,将特征值和对应的系数相乘,得到:

显然。（好好领悟理解）
  到这里为止，我们再次总结一下前面的结论：

• 矩阵的乘法可以理解为对应向量的坐标系的变换（从坐标系角度理解）
• 从特征向量的性质看，矩阵对应的一组特征向量是线性无关的，因此可以作为一组基。

  重点来了，从上面的计算我们可以看出，矩阵左乘一个向量的结果等价于矩阵的特征向量的线性组合的伸缩对对应向量的表示（好好理解下这句话）。也就是说对应向量在以矩阵特征向量为基的坐标系下进行了伸缩。也可以理解为，矩阵所充当的映射,实际上就是对特征向量的缩放,每个特征向量的缩放程度就是特征值。【参考文献5】的评论可以理解特征值和特征向量是矩阵本身的属性。

5 理解其它结论

5.1 对角化分解

参考文献【5】理解的不是很透彻，理解好了再来补充

6 参考文献

[1]特征值和特征向量的通俗解释
[2]Python计算特征值与特征向量案例
[3]特征值和特征向量到底是个啥？能做什么用？
[4]如何理解矩阵特征值和特征向量？
[5]特征值和特征向量的理解 浅显易懂 肯定有收获