MATLAB将动画演示以及将过程保存为gif动态图片

平时想要做一个动画图片来演示，本人一般有两种方法：
一种是截很多张图之后，将这些图片合成为一张gif动画；
另一种就是录屏再制作成gif，我一般是录下视频之后，使用QQ影音，里面的影音工具箱有一个制作动画的功能。
这两种方法都比较繁琐，尤其是第一种需要慢慢截自己需要的图，所以这里介绍一种在MATLAB中使用代码来保存整个动画演示过程的gif图片的方法，这样就方便很多了。

1、机器人教学

依然使用p560六轴机械臂机器人来演示，首先就是加载机器人：

startup_rvc
mdl_puma560

没有下载MATLAB，想要学习的可以查阅：MatLab的下载、安装与使用(亲测有效)
需要研究机器人的，需要下载机器人工具包：MATLAB的rvctools工具箱熟悉运动学【机械臂机器人示例】

我们使用前面学过的运动学的正解确定起始位姿和目标位姿，规划出一条运动轨迹，然后画出来：

t=[0:0.05:2];%两秒完成轨迹，步长0.05
T1 = p560.fkine(qz);%起始位姿，qz零角度
%T2 = p560.fkine(qn)
T2 = p560.fkine([pi/2 pi/3 pi/6 0 0 0]);%目标位姿
J = p560.jtraj(T1,T2,t);%生成轨迹
p560.plot(J)

接下来我们就是将这个演示的动画给保存起来，制作成一个gif的动画：

%制作动画
filename = 'demo.gif';
for i = 1:length(t)
    pause(0.01)
    p560.plot(J(i,:));
    f = getframe(gcf);  %gcf获取当前图窗的句柄，getframe捕获坐标区或图窗作为影片帧
    imind = frame2im(f); %返回与影片帧关联的图像数据
    [imind,cm] = rgb2ind(imind,256); %将 RGB 图像转换为索引图像
    if i == 1
        imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',0.1);
    else
        imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',0.1);
    end
end

制作动画的过程就是将动画的每一帧写入到gif这个动画图片里面去，原理如下：
开启动画演示，使用 gcf 函数获取当前图窗的句柄，然后通过 getframe 函数来捕获坐标区或图窗作为影片帧，再使用 frame2im 函数返回与影片帧关联的图像数据，以及使用 rgb2ind 函数将 RGB 图像转换为索引图像（此 MATLAB 函数 使用最小方差量化和抖动将 RGB 图像转换为索引图像 X。map 最多包含 n 个颜色。n 必须小于或等于 65,536。）
最后使用 imwrite 函数将图像数据写入图形文件中，这里是动画所以会一直不断的写入动态的图像数据到gif文件中。
另外这里面的for循环和if的用法，需要注意的是都需要end来匹配结束。

2、幂函数

x的一次方到x的6次方的动画演示：

x = -2:0.01:2;
n = 1:1:6;
filename = 'demo1.gif'
for i = 1:length(n)
    y = x.^(n(i));
    plot(x,y,'r','LineWidth',1)
    title(['y = x^' num2str(n(i))])
    drawnow
    frame = getframe(gcf);
    im{i} = frame2im(frame);
    [A,map] = rgb2ind(im{i},256); 
    if i == 1
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',1);%每帧播放时间
    else
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',1);
    end
end

3、正弦函数

filename = 'demo2.gif'
for i = 1:4
    x = 0:0.1:2*pi*i;
    y = sin(x);
    plot(x,y,'r','LineWidth',1)
    title('y = sinx')
    drawnow
    frame = getframe(gcf);
    im{i} = frame2im(frame);
    [A,map] = rgb2ind(im{i},256); 
    if i == 1
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',1);%每帧播放时间
    else
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',1);
    end
end

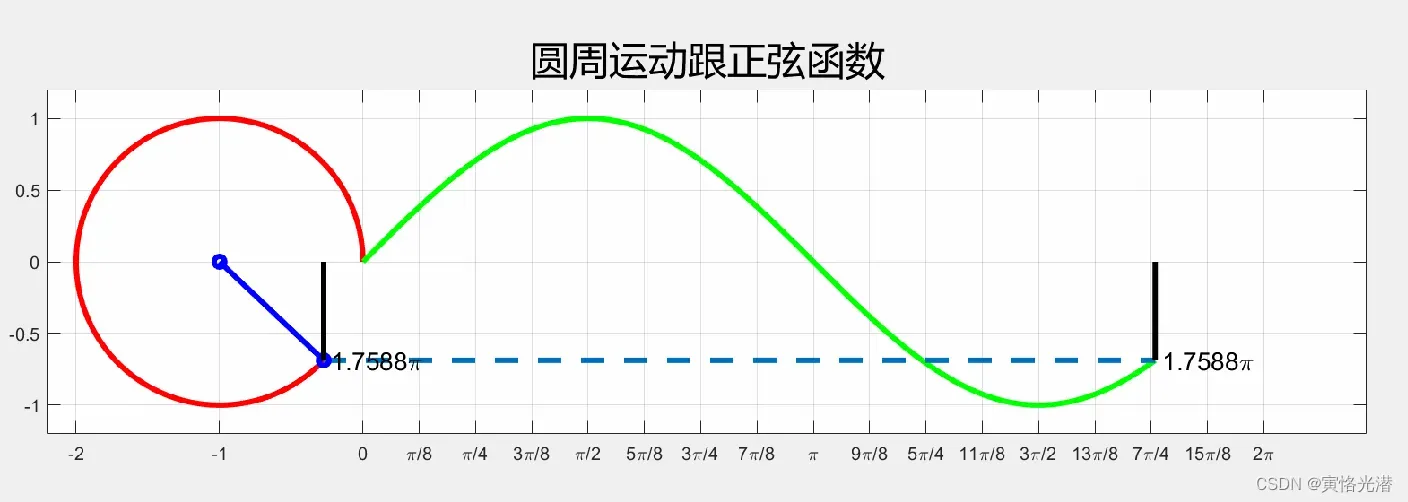
4、圆与正弦函数

圆周运动与正弦函数的关系（0到2π的一个圆也是正弦函数一个周期），所以三角函数也叫做圆函数，最初就是圆上的点做的运动而形成的轨迹吧。

theta = linspace(0,2*pi,200); 
%圆的坐标
x = cos(theta)-1;
y = sin(theta);
%正弦函数坐标
x1 = theta;
y1 = sin(x1);
 
for i = 1:length(theta)
    set(gcf,'outerposition',get(0,'screensize'));%全屏
    %圆和正弦函数之间的连接线
    connectLineX = linspace(x(i),x1(i),50);
    connectLineY = zeros(1,50)+y(i);

    AxisX = linspace(-2,10,50);
    AxisY = zeros(1,50);
    %圆中的箭头
    arrowX = [-1,x(i)];
    arrowY = [0,y(i)];
    
    %圆周上的点到横轴的垂线
    lineX = zeros(1,20)+x(i);
    lineY = linspace(0,y(i),20);
    %正弦函数上的点到横轴的垂线
    x3 = zeros(1,20)+x1(i);
    y3 = linspace(0,y1(i),20);
    %画图
    plot(x(1:i),y(1:i),'r',x1(1:i),y1(1:i),'g',connectLineX,connectLineY,'--',arrowX,arrowY,'-bo',lineX,lineY,'k',x3,y3,'k','LineWidth',3);
    text(x(i)+0.05,y(i),strcat(num2str(theta(i)/pi),'\pi'),'fontsize',14);
    text(x1(i)+0.05,y1(i),strcat(num2str(theta(i)/pi),'\pi'),'fontsize',14);
    grid on
    axis equal
    axis([-2.2 7 -1.2 1.2])
    set(gca,'XTick',[-2,-1,0:pi/8:2*pi]);
    set(gca,'xtickLabel',{'-2','-1','0','\pi/8','\pi/4','3\pi/8','\pi/2','5\pi/8','3\pi/4','7\pi/8','\pi','9\pi/8','5\pi/4','11\pi/8','3\pi/2','13\pi/8','7\pi/4','15\pi/8','2\pi'});
    title('圆周运动跟正弦函数','fontsize',22,'fontname','微软雅黑')
    drawnow
    f=getframe(gcf);
    imind=frame2im(f);
    [imind,cm] = rgb2ind(imind,256);
    if i == 1
        imwrite(imind,cm,'sin.gif','GIF', 'Loopcount',inf,'DelayTime',0.02);
    else
        imwrite(imind,cm,'sin.gif','GIF','WriteMode','append','DelayTime',0.02);
    end
end

由于动画超过5M,上传不过，截个图如下：

PS画圆：

t=0:0.1:2*pi
x = cos(t);
y = sin(t);
plot(x,y)
或者
ezplot('x^2+y^2=1')