如何判断一个正定矩阵？
1、所有顺序主子式大于0.
2、特征值全为正。
3、标准型中主对角元素全为>0。
4、正惯性指数等于n。
5、合同于单位矩阵等于E（规范形为E）
6、存在可逆矩阵C使=该矩阵。
有可逆矩阵X，
为什么为半正定矩阵？
如果有一个的实对称矩阵定义为A，一个n维的vector定义为x，如果满足
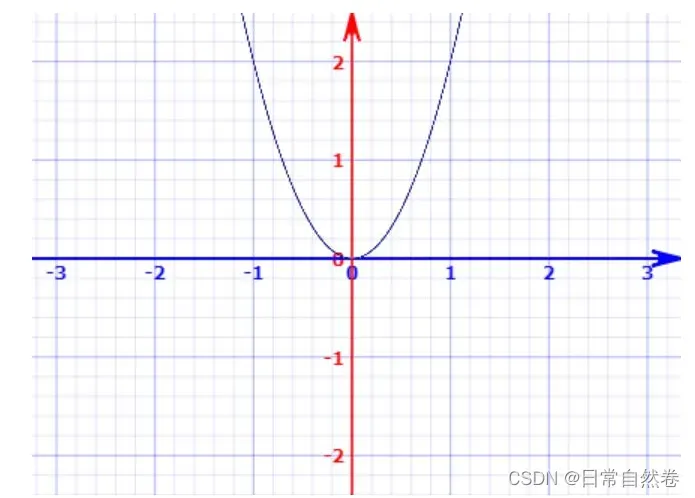
，就可以把实对称矩阵A定义为半正定矩阵，我们从数学函数的角度来理解，初中二次函数
是恒定大于等于0的，我们可以把·
理解为
的高纬度映射，因为A在二次函数中的作用是改变图形的开口大小，并不影响值域范围，所以我们A换成n*n的单位矩阵I，单位矩阵I（单位矩阵也为实对称矩阵），I的的一维的矩阵是1，变成了y=
,他是核定大于等于0的，映射到高维度，
，又因为I可以去掉，所以
也是恒定大于0的，所以
是半阵。
文章出处登录后可见！
已经登录？立即刷新
